V. Введение в пространственную статистику (1)#

Пространственная статистика точек (Spatial Point Analysis)#

Пространственная статистика точек — это набор методов для анализа распределения точек в пространстве. Эти методы позволяют изучать закономерности и кластеризацию точек, а также проводить проверку гипотез о случайности распределения объектов.

В этом разделе мы изучим данные о ДТП с Санкт-Петербурге за 2023 год

В дополнение к основной теме мы познакомимся с библиотеками seaborn и contextily. Seaborn - крутая библиотека для визуализации на основн matplotlib. Contextily помогает добавлять базовые карты (подложки).

Импортируем библиотеки

import geopandas as gpd
from shapely.geometry import Point
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial import distance
import contextily
import seaborn
import osmnx as ox

Читаем данные о ДТП и перепроецируем в подходящую UTM-зону

accidents = gpd.read_file('data/spb_dtp.gpkg')

target_utm = accidents.estimate_utm_crs()
accidents_utm = accidents.to_crs(target_utm)

/Library/Frameworks/Python.framework/Versions/3.10/lib/python3.10/site-packages/geopandas/io/file.py:383: FutureWarning: errors='ignore' is deprecated and will raise in a future version. Use to_datetime without passing `errors` and catch exceptions explicitly instead
  as_dt = pd.to_datetime(df[k], errors="ignore")

1. Расстояние до ближайшего соседа (Nearest Neighbor Distance)#

Этот метод используется для измерения расстояний между точками и анализа их пространственного распределения

# Расчёт расстояний до ближайшего соседа
distances = []
for point in accidents_utm.geometry:
    dist = accidents_utm.geometry.distance(point)
    dist = dist[dist > 0]  # исключаем нулевые значения
    distances.append(np.min(dist))

# Визуализация гистроаммы распределения
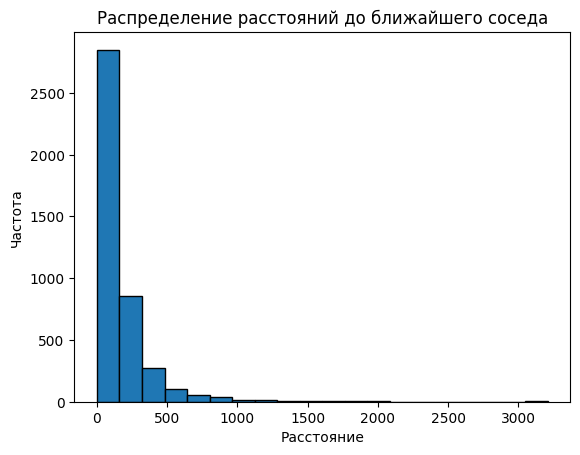
plt.hist(distances, bins=20, edgecolor='black')
plt.title("Распределение расстояний до ближайшего соседа")
plt.xlabel("Расстояние")
plt.ylabel("Частота")
plt.show()
../_images/23a8cbf5e24e3272b992dea8c2a429289c84a495693759472291a3673bb48afc.png

2. Nearest Neighbour Index#

NNI (Nearest Neighbor Index, индекс ближайшего соседа) — это статистическая мера, которая позволяет оценить, насколько равномерно распределены объекты в пространстве. Мы с ним уже познакомились пару недель назад.

NNI рассчитывается как отношение двух величин:

  • наблюдаемого среднего расстояния до ближайшего соседа между всеми объектами в выборке (robs)

  • ожидаемого среднего расстояния между точками при полностью случайном (гомогенном пуассоновском) распределении (rexp)

Интерпретация значения:

  • NNI < 1 — объекты имеют склонность к кластеризации (сосредоточены ближе друг к другу, чем при случайном распределении);

  • NNI ≈ 1 — распределение близко к случайному;

  • NNI > 1 — объекты расположены более равномерно (регулярно), чем при случайном распределении.

#  Вычисление среднего расстояния до ближайшего соседа
average_nearest_neighbor_distance = np.mean(distances)

# Вычисление площади Санкт-Петербурга
spb_area = ox.geocode_to_gdf("Санкт-Петербург")
spb_area = spb_area.to_crs(spb_area.estimate_utm_crs())
spb_area = spb_area.area.values[0] 

# Расчет ожидаемого среднего расстояния для случайного распределения точек
n = len(distances)
expected_mean_distance = 0.5 * np.sqrt(spb_area / n)

# Расчет NNI
NNI = average_nearest_neighbor_distance / expected_mean_distance
NNI

0.42037362841769255

Альтернативно можно подумать о том, как считать площадь территории без учеба административных границ, например, создавая выпуклую оболчку вокруг точек:

  1. Создание выпуклой оболочки (convex hull) convex_hull = accidents.geometry.unary_union.convex_hull

  2. Создание нового GeoDataFrame для выпуклой оболочки convex_hull_gdf = gpd.GeoDataFrame( {‘geometry’: [convex_hull]}, crs=accidents.crs # Убедитесь, что координатная система одинакова )

Но это тоже неидеальный вариант для Санкт-Петербурга, почему?

3. Визуальное исследование точек#

seaborn.jointplot(x=accidents_utm.geometry.x, y=accidents_utm.geometry.y, data=accidents_utm, s=0.5);
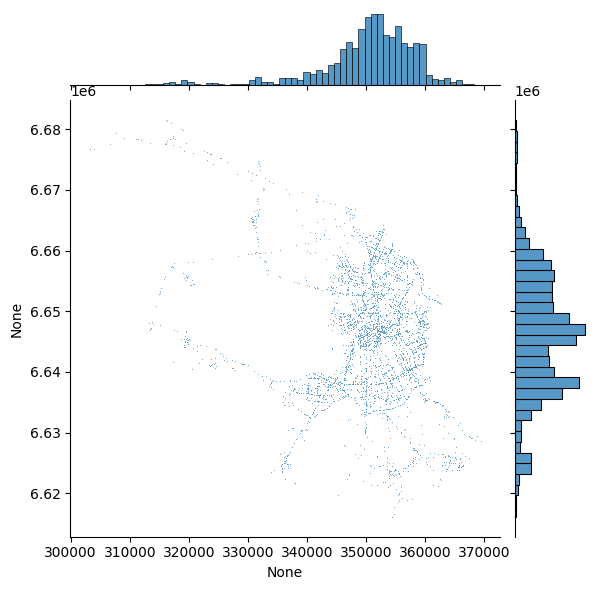
../_images/15f2d7e4e35f27876dcc635cd8281c9448d82406fb5f923aedc3e53c382ca7b3.png

Это хороший старт: благодаря гистроамме мы видим, что точки склонны сосредотачиваться в центре города и на юге. Но без знания города, тяжело оценить размещение объектов. Давайте добавим на карту basemap

Сделаем это с помощью библиотеки contextily

joint_axes = seaborn.jointplot(
    x=accidents_utm.geometry.x, y=accidents_utm.geometry.y, data=accidents_utm, s=0.5
)
contextily.add_basemap(
    joint_axes.ax_joint,
    source=contextily.providers.CartoDB.PositronNoLabels,
    crs=target_utm,
)
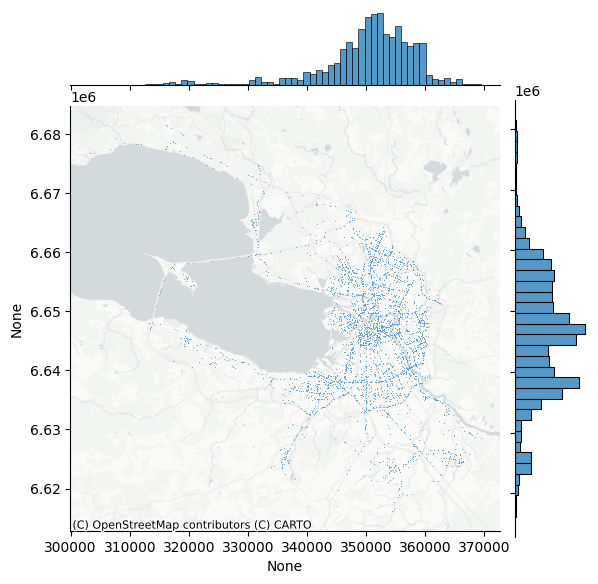
../_images/114b5926a0682f55757e3e90e5dfb2b7dbf6ad1b5e115cc4e94f7931eb61bebd.png

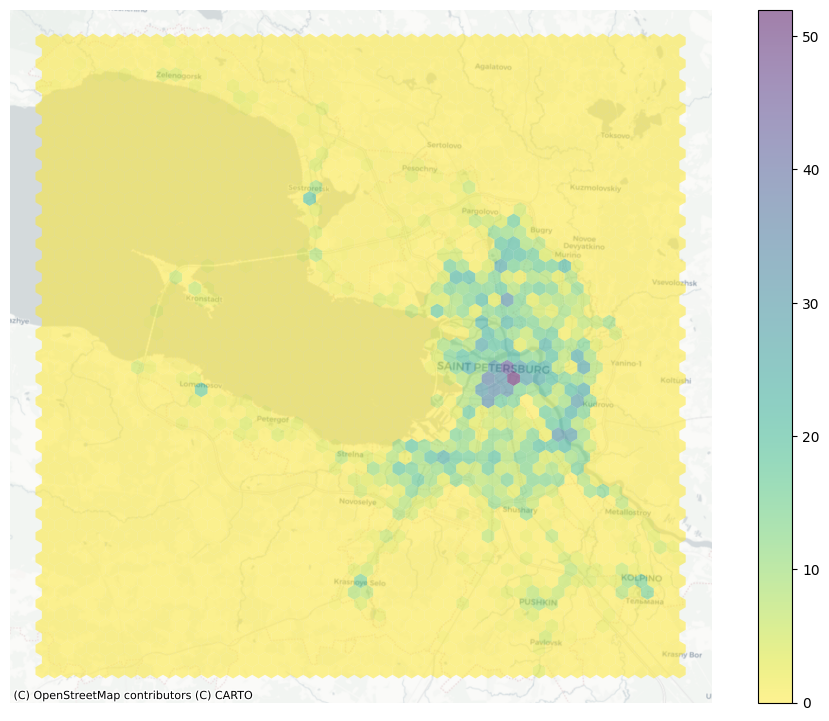
4. Плотность на основе регулярной сетки#

Отобразим плотность на основе ячеек регулярной сетки

Когда слишком много точек сосредоточено в одной области, плотное наложение точек затрудняет выявление паттернов. Например, на карте видно, что в центре города сосредоточено очень много аварий, но трудно понять, является ли это равномерным распределением или есть места с особенно высокой концентрацией. Поэтому можно наложить точки на сетку и наглядно увидеть концентрацию

# Set up figure and axis
f, ax = plt.subplots(1, figsize=(12, 9))
# Generate and add hexbin with 50 hexagons in each
# dimension, no borderlines, half transparency,
# and the reverse viridis colormap
hb = ax.hexbin(
    accidents_utm.geometry.x,
    accidents_utm.geometry.y,
    gridsize=50,
    linewidths=0,
    alpha=0.5,
    cmap="viridis_r",
)
# Add basemap
contextily.add_basemap(
    ax, source=contextily.providers.CartoDB.Positron,
    crs=target_utm,
)
# Add colorbar
plt.colorbar(hb)
# Remove axes
ax.set_axis_off()
../_images/e374ea4966c31862e569b4649c748b64647361d5df8f7b32278442d7569ea6fc.png

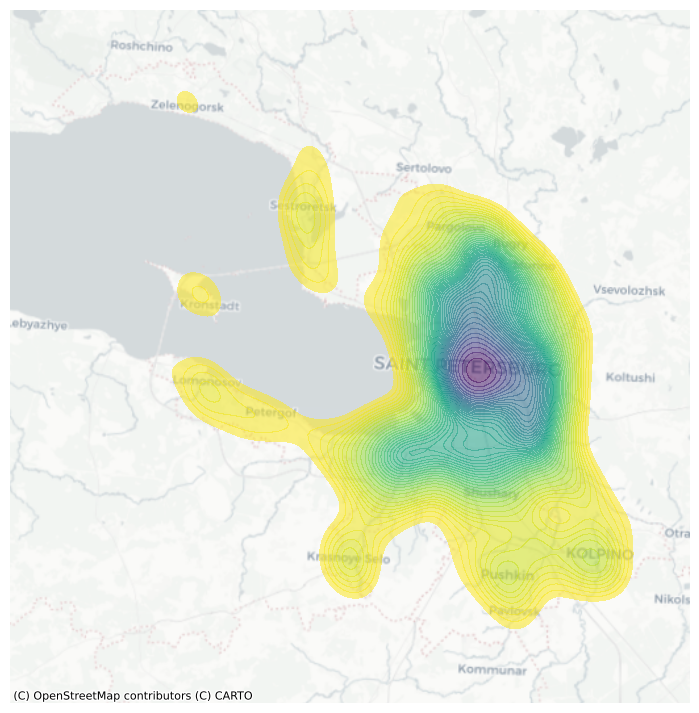
5. Плотностная модель (Kernel Density Estimation)#

Альтернативный подход оценка плотности с помощью KDE (kernel density estimation): эмпирическая аппроксимация функции плотности вероятности.

Вместо того чтобы накладывать сетку квадратов или гексагонов и подсчитывать, сколько точек попадает в каждую, KDE накладывает сетку точек на интересующее пространство и размещает функции ядра, которые учитывают точки вокруг них с разным весом в зависимости от расстояния. Эти подсчеты затем агрегируются, чтобы создать глобальную поверхность с вероятностью плотности.

# Set up figure and axis
f, ax = plt.subplots(1, figsize=(9, 9))
# Generate and add KDE with a shading of 50 gradients
# coloured contours, 75% of transparency,
# and the reverse viridis colormap

seaborn.kdeplot(
    x=accidents_utm.geometry.x,
    y=accidents_utm.geometry.y,
    levels=50,
    fill=True,
    alpha=0.55,
    cmap="viridis_r",
    ax=ax
)
# Add basemap
contextily.add_basemap(
    ax, source=contextily.providers.CartoDB.Positron,
    crs=target_utm,
)
# Remove axes
ax.set_axis_off()
../_images/14c34416c04ee08f33c108ad75ffda7898341a77f12209eae06a3fb8e9ded6c3.png

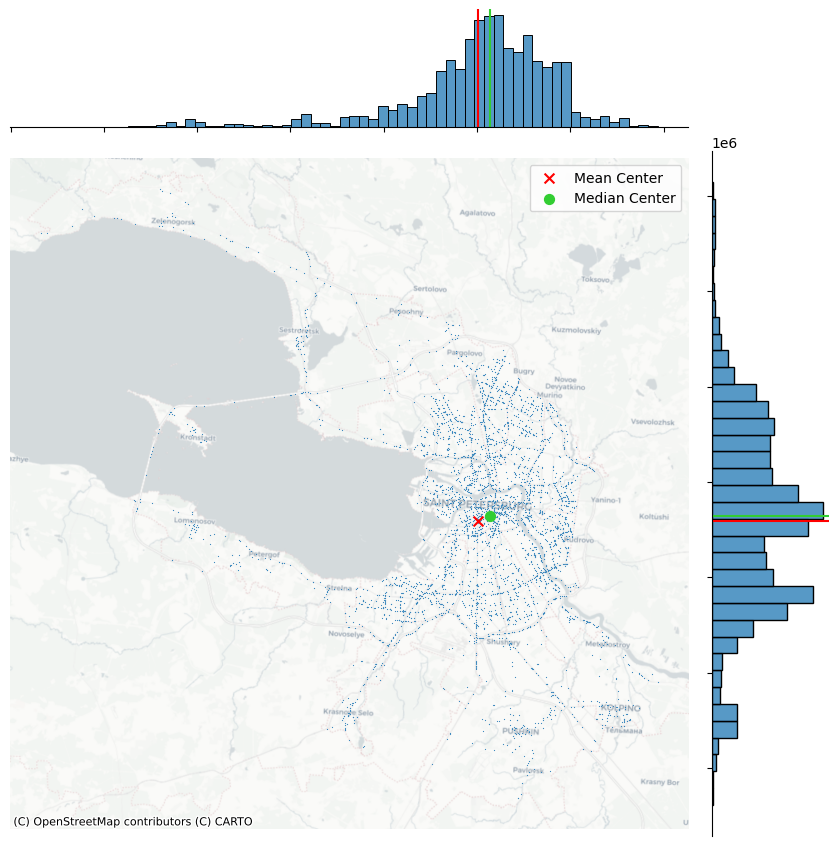
6. Центрография#

Это раздел пространственного анализа, посвящённый выявлению «центров» точечного распределения и оценке его структуры. Главные задачи центрографии:

  • Определить «центр тяжести» набора точек, чтобы получить представление о том, где сосредоточена максимальная масса событий (например, аварий, преступлений, точек продаж и т. д.)

  • Сравнить разные распределения: сместился ли центр события со временем, отличается ли он между двумя категориями объектов.

  • Оценить степень разброса: помимо центра важно знать, насколько распределены точки вокруг него.

from pointpats import centrography

Определим средний и медианный центр нашего набора данных

# Извлечение координат x и y
accidents_utm["x"] = accidents_utm.geometry.x
accidents_utm["y"] = accidents_utm.geometry.y

# Вычисление среднего центра (mean center)
mean_center = centrography.mean_center(accidents_utm[["x", "y"]])

# Вычисление медианного центра (Euclidean median)
med_center = centrography.euclidean_median(accidents_utm[["x", "y"]])

Отобразим на карте

# Generate scatterplot
joint_axes = seaborn.jointplot(
    x="x", y="y", data=accidents_utm, s=0.75, height=9
)
# Add mean point and marginal lines
joint_axes.ax_joint.scatter(
    *mean_center, color="red", marker="x", s=50, label="Mean Center"
)
joint_axes.ax_marg_x.axvline(mean_center[0], color="red")
joint_axes.ax_marg_y.axhline(mean_center[1], color="red")
# Add median point and marginal lines
joint_axes.ax_joint.scatter(
    *med_center,
    color="limegreen",
    marker="o",
    s=50,
    label="Median Center"
)
joint_axes.ax_marg_x.axvline(med_center[0], color="limegreen")
joint_axes.ax_marg_y.axhline(med_center[1], color="limegreen")
# Legend
joint_axes.ax_joint.legend()
# Add basemap
contextily.add_basemap(

    joint_axes.ax_joint, source=contextily.providers.CartoDB.Positron, crs= target_utm,
)
# Clean axes
joint_axes.ax_joint.set_axis_off()
# Display
plt.show()
../_images/66077923b78bd60c3113657219ed10dd7bbb697d84a19c70badcc84afecbec9f.png

Посчитаем стандартное расстояние (пространственный аналог среднего отклонения) - мреднее расстояние точек от центра

centrography.std_distance(accidents_utm[["x", "y"]])

13387.089449467901

Итог#

В этом резделе мы познакомились с основами анализа пространственного распределения точек на примере данных ДТП в Санкт-Петербурге.