III. Инструменты геоанализа (2)

На этой неделе мы продолжим занкомиться с разными инструментами пространственного анализа: научимся агрегировать атрибутивную информацию, познакомимся с Диаграммой Вороного и Индексом ближайшего соседа

Эти навыки помогут дополнить анализ исторической вспышки холеры в Лондоне (1854) – второй проект на нашем курсе.

0. Импортируем нужные библиотеки

import pandas as pd      
import geopandas as gpd   
import osmnx as ox   

import matplotlib.pyplot as plt  
import matplotlib as mpl   

from shapely.ops import voronoi_diagram  
from shapely.geometry import MultiPoint  

import numpy as np  
from scipy.spatial.distance import cdist

pandas – фундаментальная библиотека для работы с табличными данными в Python. Предоставляет высокоуровневые структуры данных (Series, DataFrame) и богатый набор инструментов для загрузки, очистки, агрегации, группировки и преобразования данных.

GeoPandas – надстройка над pandas, расширяющая возможности DataFrame для работы с геометрией. Хранит объекты геометрии (точки, линии, полигоны) в специальном столбце geometry и предоставляет методы для пространственных операций (буферизация, объединение, объединение по пространственному признаку).

osmnx – библиотека для загрузки и анализа данных OpenStreetMap. Позволяет легко получать графы улиц, точки интереса и другие геоданные напрямую из OSM, а также выполнять маршрутизацию, визуализацию и базовый пространственный анализ городских сетей.

Shapely – библиотека для создания и операций над геометрическими примитивами (точки, линии, полигоны). Предоставляет методы для объединения, пересечения, измерения расстояний и вычисления буферных зон, а также инструменты для генерации диаграмм Вороного (voronoi_diagram) и работы с множеством точек (MultiPoint).

numpy – основная библиотека для работы с многомерными массивами и матрицами в Python. Обеспечивает быстродействие за счёт векторизированных операций, а также содержит базовые функции для линейной алгебры, статистики и элементарных математических преобразований.

scipy.spatial.distance – модуль из SciPy для вычисления попарных расстояний между наборами точек. Содержит функции для различных метрик (Евклидово расстояние, Манхэттенское и др.) и умеет возвращать матрицы расстояний для последующего анализа.

matplotlib.pyplot – модуль визуализации, вдохновлённый MATLAB. Позволяет строить 2D-графики (линии, гистограммы, scatter-плоты), настраивать оформление, добавлять подписи, легенды и работать с осями.

matplotlib – базовый пакет для создания статических, анимированных и интерактивных визуализаций в Python. Содержит механизмы настройки стилей, колормэппингов и управления элементами фигуры (шрифты, размеры, отступы).

contextily – утилита для подложек карт (tile basemaps) в matplotlib. Позволяет легко добавить тайловые слои (OpenStreetMap, Stamen и др.) под ваши геоплоты, автоматически приводя проекции в соответствие.

1. Агрегирование атрибутивной информации

На прошлой неделе мы научились агрегировать точечный слой по полигонам — подсчитывать число точек. Сегодня разберёмся, как агрегировать атрибуты объектов

Прочитаем данные об МКД в Санкт-Петербурге и о границах районов

#Данные с округами в Санкт-Петербурге в формате geopackage
admin_okrug = gpd.read_file('data/spb_admin.gpkg', layer="okrug")

#МКД Санкт-Петербурга в формате csv
mkd = pd.read_csv('data/spb_mkd.csv')
#Разбиваем поле с координатами на два - 'lat' -- широта; 'lon' -- долгота
mkd[['lat', 'lon']] = mkd['coordinates'].str.split(',', expand=True).astype(float)
#На основе DataFrame создаем GeoDataFrame, определяя геометрию на основе координат
mkd_gdf = gpd.GeoDataFrame(mkd, geometry=gpd.points_from_xy(mkd['lon'], mkd['lat']), crs=4326)

Давайте посмотрим, какая атрибутивная информация есть в слое с МКД

# такая запись помогает нам не просто показать первые строки, но и транспонировать таблицу, чтобы увидеть сразу все столбцы
mkd_gdf.head().T

	0	1	2	3	4
addr_street	Киевская ул.	Лесной пр.	Новочеркасский пр.	Полярников ул.	Ж. Егоровой ул.
addr_number	24/22	39	41/14	12	10
addr_building	NaN	1-3	NaN	NaN	1
addr_letter	А	А	A	Б	А
addr_district	Московский	Выборгский	Красногвардейский	Невский	Выборгский
comm_type	2 комн., 3 комн., 5 комн., 6 комн.	2 комн., 3 комн., 4 комн., 5 комн.	2 комн., 3 комн., 5 комн., 6 комн., 7 комн.	2 комн., 3 комн., 4 комн.	2 комн., 3 комн.
comm_num	3, 18, 1, 1	11, 29, 18, 2	5, 8, 4, 2, 1	1, 6, 8	8, 13
comm_room_num	6, 54, 5, 6	22, 87, 72, 10	10, 24, 20, 12, 7	2, 18, 32	16, 39
data_series	Индивидуальный	индивидуальный	индивидуальный	инд	1 ЛГ 606
data_buildingdate	1930	1932	1957	1951	1985
data_reconstructiondate	NaN	NaN	NaN	NaN	NaN
data_buildingarea	6335.5	10793.1	13817.8	6376.6	15142.1
data_livingarea	4654.0	9291.2	10613.5	4734.79	14039.5
data_nonolivingarea	987.5	481.7	898.6	209.5	0.0
data_stairs	11.0	15.0	5.0	5.0	7.0
data_storeys	5.0	5.0	7.0	6.0	9.0
data_residents	302.0	575.0	387.0	250.0	713.0
data_mansardarea	NaN	NaN	NaN	NaN	NaN
eng_heatingcentral	0.0	1.0	1.0	1.0	1.0
eng_heatingauto	1.0	0.0	0.0	0.0	0.0
eng_heatingfire	0.0	0.0	0.0	0.0	0.0
eng_hotwater	0.0	0.0	0.0	0.0	1.0
eng_hotwatergas	1.0	1.0	1.0	1.0	0.0
eng_hotwaterwood	0.0	0.0	0.0	0.0	0.0
eng_electro	1.0	1.0	1.0	1.0	1.0
eng_gascentral	1.0	1.0	1.0	1.0	0.0
eng_gasnoncentral	0.0	0.0	0.0	0.0	0.0
eng_refusechute	0.0	0.0	1.0	1.0	1.0
flat_type	1 комн., 2 комн., 3 комн.	2 комн., 3 комн., 4 комн., 5 комн.	2 комн., 3 комн., 5 комн.	1 комн., 2 комн., 3 комн., 4 комн.	1 комн., 2 комн., 3 комн., 4 комн.
flat_num	1, 32, 25	50, 29, 5, 2	69, 54, 2	4, 34, 14, 10	49, 70, 96, 8
flat_room_num	1, 64, 75	100, 87, 20, 10	138, 162, 10	4, 68, 42, 40	49, 140, 288, 32
internal_num	7.0	1.0	NaN	NaN	NaN
lift_exploitfromdate	NaN	NaN	1981	NaN	1985
lift_reconstructiondate	NaN	NaN	2003.2004	NaN	NaN
lift_repairdate	NaN	NaN	NaN	NaN	NaN
outclean_all	5400.0	3076.0	7675.0	3818.0	9072.0
param_crdate	02.02.2011	05.03.2009	05.03.2009	07.02.2013	07.12.2008
param_ukname	ООО "Жилкомсервис № 1 Московского района"	ООО "Жилкомсервис № 1 Выборгского района"	ТСЖ "Лира"	ООО "Жилкомсервис № 2 Невского района"	ООО "Жилкомсервис № 1 Выборгского района"
param_failure	0.0	0.0	0.0	0.0	0.0
repair_year	2007; 2008; 2008; 2014; 2015; 2015	2005; 2011; 2017; 2018	2002; 2003; 2004; 2006; 2006; 2008; 2010; 2013	2007; 2007; 2012	1996; 2011; 2012; 2012
repair_job	Ремонт или замена системы канализования и водо...	Ремонт или замена системы холодного водоснабже...	Ремонт трубопровода (розлива) теплоснабжения в...	Ремонт или замена системы отопления; Ремонт ил...	Благоустройство придомовой территории; Ремонт ...
rfc_shaftcount	NaN	NaN	17.0	NaN	7.0
roof_metalarea	2108.0	3091.0	3150.0	1579.0	NaN
seng_liftcount	NaN	NaN	5.0	5.0	7.0
seng_pzu	11.0	6.0	5.0	5.0	7.0
special_basementarea	978.0	761.0	391.0	444.0	2262.0
number	1	2	3	4	5
address	г.Санкт-Петербург, Киевская улица, дом 24/22, ...	г.Санкт-Петербург, Лесной проспект, дом 39, ко...	г.Санкт-Петербург, Новочеркасский проспект, до...	г.Санкт-Петербург, улица Полярников, дом 12, л...	г.Санкт-Петербург, улица Жени Егоровой, дом 10...
coordinates	59.903573417,30.32885093	59.981339024,30.344940571	59.92930475,30.410388758	59.875888506,30.436156571	60.064144092,30.311062773
lat	59.903573	59.981339	59.929305	59.875889	60.064144
lon	30.328851	30.344941	30.410389	30.436157	30.311063
geometry	POINT (30.32885093 59.903573417)	POINT (30.344940571 59.981339024)	POINT (30.410388758 59.92930475)	POINT (30.436156571 59.875888506)	POINT (30.311062773 60.064144092)

У нас, к сожалению, нет документации с описанием названий полей, но мы +- можем догадываться, какая именно информация содержится в полях.

Из интересной информации, которую бы мы хотели посмотреть по каждому из округов можно выбрать: data_buildingdate - год постройки;

Давайте для каждого района посчитаем средний, медианный, самый ранний и самый поздний год постройки МКД

Первые шаги будут аналогичны тем, которые мы выполняли на прошлой неделе при подсчете кол-ва точек по ячейкам регулярной сетки

Шаг1: Выполняем пространственное объединение (Spatial Join)

Пересекаем точки с кафе и полигоны регулярной сетки (не забываем, что слои должны быть в одной системе координат)

# sjoin: определяем, в какой округ попадает каждый из МКД
mkd_in_okrug = gpd.sjoin(mkd_gdf, admin_okrug, predicate="within", how="left")

mkd_in_okrug.head()

	addr_street	addr_number	addr_building	addr_letter	addr_district	comm_type	comm_num	comm_room_num	data_series	data_buildingdate	...	special_basementarea	number	address	coordinates	lat	lon	geometry	index_right	NAME	Popul
0	Киевская ул.	24/22	NaN	А	Московский	2 комн., 3 комн., 5 комн., 6 комн.	3, 18, 1, 1	6, 54, 5, 6	Индивидуальный	1930	...	978.0	1	г.Санкт-Петербург, Киевская улица, дом 24/22, ...	59.903573417,30.32885093	59.903573	30.328851	POINT (30.32885 59.90357)	61	округ Московская застава	51624.0
1	Лесной пр.	39	1-3	А	Выборгский	2 комн., 3 комн., 4 комн., 5 комн.	11, 29, 18, 2	22, 87, 72, 10	индивидуальный	1932	...	761.0	2	г.Санкт-Петербург, Лесной проспект, дом 39, ко...	59.981339024,30.344940571	59.981339	30.344941	POINT (30.34494 59.98134)	72	округ Сампсониевское	41330.0
2	Новочеркасский пр.	41/14	NaN	A	Красногвардейский	2 комн., 3 комн., 5 комн., 6 комн., 7 комн.	5, 8, 4, 2, 1	10, 24, 20, 12, 7	индивидуальный	1957	...	391.0	3	г.Санкт-Петербург, Новочеркасский проспект, до...	59.92930475,30.410388758	59.929305	30.410389	POINT (30.41039 59.92930)	87	округ Малая Охта	46981.0
3	Полярников ул.	12	NaN	Б	Невский	2 комн., 3 комн., 4 комн.	1, 6, 8	2, 18, 32	инд	1951	...	444.0	4	г.Санкт-Петербург, улица Полярников, дом 12, л...	59.875888506,30.436156571	59.875889	30.436157	POINT (30.43616 59.87589)	89	Ивановский округ	29833.0
4	Ж. Егоровой ул.	10	1	А	Выборгский	2 комн., 3 комн.	8, 13	16, 39	1 ЛГ 606	1985	...	2262.0	5	г.Санкт-Петербург, улица Жени Егоровой, дом 10...	60.064144092,30.311062773	60.064144	30.311063	POINT (30.31106 60.06414)	56	округ Шувалово-Озерки	112436.0

5 rows × 55 columns

В атрибутивной таблице выше - все поля, которые идут после “geometry” – атрибутивная информация из слоя с округами, в зависимости от того, в какой округ попадает та или иная точка

Шаг2: Рассчитываем статистику

Группируем данные на основе их попадания в тот или иной округ (например, по полю index_right) и рассчитываем значения

Важно: поскольку мы хотим рассчитывать количественную статистику, необходимо проверить типы данных полей (data_buildingdate, data_residents) и убедиться, что они имеют числовой тип или преобразовать их в числовой

# 1. Посмотреть исходные типы
print("До преобразования:")
print(mkd_in_okrug[['data_buildingdate']].dtypes)

# 2. Преобразование

mkd_in_okrug['data_buildingdate'] = pd.to_numeric(mkd_in_okrug['data_buildingdate'], errors='coerce')

# 3. Проверка — типы после
print("\nПосле преобразования:")
print(mkd_in_okrug['data_buildingdate'].dtypes)

До преобразования:
data_buildingdate    object
dtype: object

После преобразования:
float64

Отлично! Теперь мы точно можем рассчитывать количественную статистику на основе этого поля

Рассчитаем средний год постройки МКД в разных округах

build_year_mean = mkd_in_okrug.groupby('index_right')['data_buildingdate'].mean()

# Добавляем в данные поля с средним годом постройки в слой с округами
admin_okrug['build_year_mean'] = build_year_mean

# Смотрим на результат
admin_okrug.explore(column='build_year_mean', cmap='YlGnBu', tiles='CartoDB positron')

Make this Notebook Trusted to load map: File -> Trust Notebook

Выглядит очень интересно и правдоподобно :)

По аналогии посчитаем медианный год постройки, а также самый ранний и самый поздний

build_year_median = mkd_in_okrug.groupby('index_right')['data_buildingdate'].median()
build_year_min = mkd_in_okrug.groupby('index_right')['data_buildingdate'].min()
build_year_max = mkd_in_okrug.groupby('index_right')['data_buildingdate'].max()

# Добавляем в данные соответсвующие поля
admin_okrug['build_year_median'] = build_year_median
admin_okrug['build_year_min'] = build_year_min
admin_okrug['build_year_max'] = build_year_max

Отобразим 4 показателя вместе для сравнения

metrics = [
    ('build_year_mean', 'Средний год постройки'),
    ('build_year_median', 'Медианный год постройки'),
    ('build_year_min', 'Самый ранний год постройки'),
    ('build_year_max', 'Самый поздний год постройки'),
]

# Общий диапазон для всех карт
vmin = admin_okrug[[m for m, _ in metrics]].min().min()
vmax = admin_okrug[[m for m, _ in metrics]].max().max()

# Создаём одну фигуру с 1 строкой и 4 столбцами
fig, axes = plt.subplots(1, 4, figsize=(20, 5), constrained_layout=True)

# Создаём общий нормализатор и мэппер для цветовой шкалы
norm = mpl.colors.Normalize(vmin=vmin, vmax=vmax)
cmap = mpl.cm.viridis  # или любая другая

for ax, (metric, title) in zip(axes, metrics):
    admin_okrug.plot(
        column=metric,
        ax=ax,
        cmap=cmap,
        norm=norm,
        linewidth=0.5,
        edgecolor='gray'
    )
    ax.set_title(title, fontsize=12)
    ax.axis('off')

# Общая colorbar
sm = mpl.cm.ScalarMappable(cmap=cmap, norm=norm)
sm._A = []  # пустой массив, чтобы colorbar работал
cbar = fig.colorbar(sm, ax=axes.tolist(), orientation='horizontal',
                    fraction=0.05, pad=0.02)
cbar.set_label('Год постройки', fontsize=12)

plt.show()

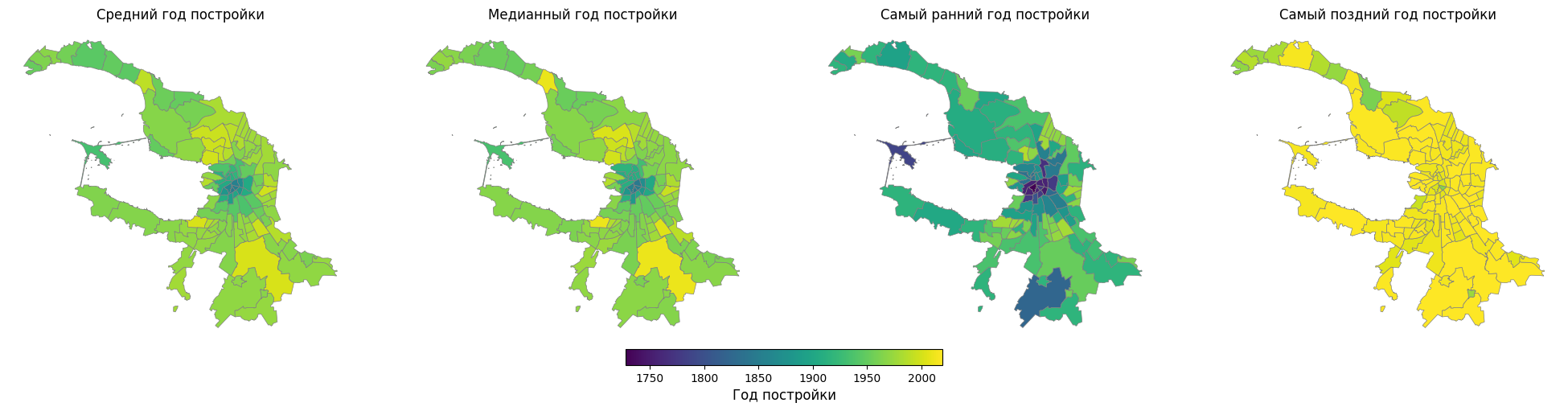
Красота!

2. Построение диаграммы Вороного

Диаграмма Вороного (или разбиение Вороного) — это разбиение пространства на ячейки по следующему правилу: каждой точке-генератору (site) сопоставляется такая область, что любая точка внутри этой области ближе к нему, чем к любой другой.

Загрузим данные станций метро и разобьём территорию Петербурга на области Вороного: каждая область соответствует ближайшей станции

#Прочитаем данные о станциях метро
metro = gpd.read_file('data/spb_metro.geojson')

#Создадим полигон с границами города на основе admin_okrug c помощью инструмента dissolve
admin_border = admin_okrug.dissolve()


# Построим карту с двумя слоями
fig, ax = plt.subplots(figsize=(8, 8))
# Сначала — граница города
admin_border.plot(ax=ax, color='none', edgecolor='black', linewidth=1)
# Затем — станции метро
metro.plot(ax=ax, color='red', markersize=10, label='Станции метро')
# Оформление
ax.set_title('Граница СПб и станции метро', fontsize=14)
ax.axis('off')
ax.legend()

plt.tight_layout()
plt.show()

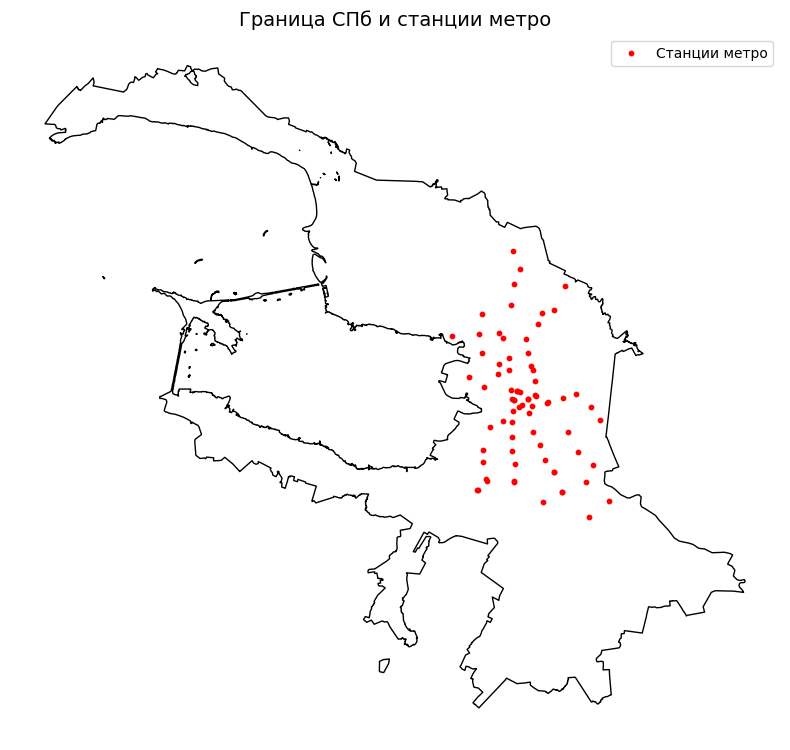
Строим диаграмму Вороного

# 1. Собираем все точки-генераторы в один объект MultiPoint
#    Здесь каждая станция метро — это точка (Point).
#    .geometry.tolist() возвращает список shapely-геометрий.
points_mp = MultiPoint(metro.geometry.tolist())

# 2. Генерируем диаграмму Вороного по точечному набору станций метро,
#    ограничивая все ячейки рамкой города (envelope) — чтобы полигоны
#    не выходили за пределы Санкт-Петербурга.
vor = voronoi_diagram(points_mp, envelope=admin_border.geometry.iloc[0])

# 3. Создаём GeoDataFrame из полигонов Вороного:
#    конвертируем коллекцию геометрий в список и передаём его в GeoDataFrame,
#    сохраняя исходную систему координат (CRS) станций метро.
cells = list(vor.geoms)
vor_gdf = gpd.GeoDataFrame(geometry=cells, crs=metro.crs)

# 4. Визуализация результата
fig, ax = plt.subplots(figsize=(8, 8))

# 4.1. Рисуем полигоны диаграммы Вороного
#      cmap='gist_ncar' — качественная палитра с множеством цветов.
#      edgecolor='white' и alpha=0.6 делают границы полигонов чёткими,
#      но сохраняют прозрачность для наглядности.
vor_gdf.plot(
    ax=ax,
    cmap='gist_ncar',
    edgecolor='white',
    alpha=0.6
)

# 4.2. Наносим станции метро поверх полигонов
#      color='red' и markersize задают красные точки нужного размера.
metro.plot(
    ax=ax,
    color='red',
    markersize=8,
    label='Станции метро'
)

# 4.3. Рисуем контур границы города
#      boundary.plot рисует только линию границы без заливки.
admin_border.boundary.plot(
    ax=ax,
    color='black',
    linewidth=1,
    label='Граница СПб'
)

# 5. Настройка оформления
ax.set_title(
    "Диаграмма Вороного по станциям метро СПб (Shapely)",
    fontsize=14
)
ax.axis('off')   # отключаем оси, они не нужны на карте
ax.legend()      # выводим легенду по точкам и границе

plt.tight_layout()
plt.show()

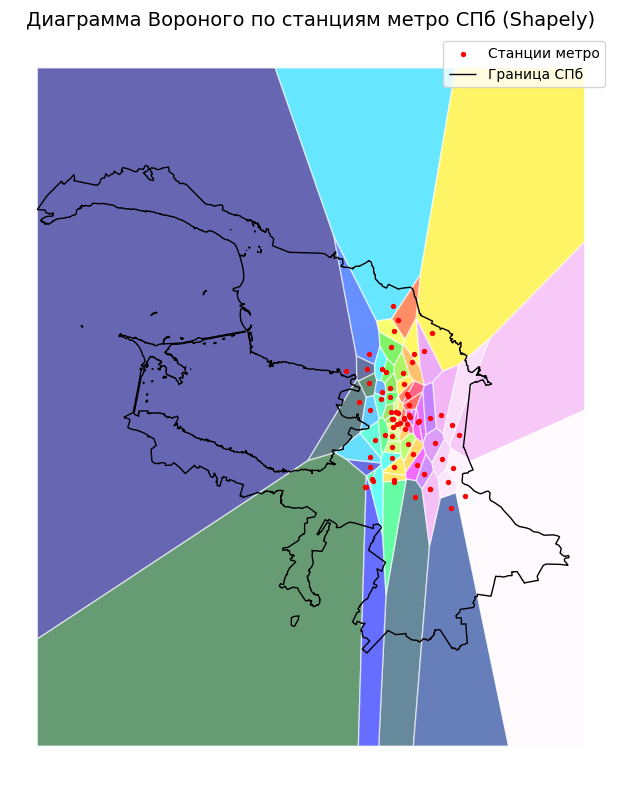
Обрежем диаграмму Вороного по границам города

# 1.Выполняем обрезку (clip) полигонов Вороного по границе Санкт-Петербурга
clipped_vor = gpd.clip(vor_gdf, admin_border.geometry.unary_union)

# 2. Визуализируем результат
fig, ax = plt.subplots(figsize=(8, 8))

# 2.1. Рисуем обрезанные полигоны Вороного
clipped_vor.plot(
    ax=ax,
    cmap='gist_ncar',
    edgecolor='white',
    alpha=0.6
)

# 2.2. Наносим станции метро поверх полигонов
metro.plot(
    ax=ax,
    color='red',
    markersize=8,
    label='Станции метро'
)

# 2.3. Рисуем контур границы города
admin_border.boundary.plot(
    ax=ax,
    color='black',
    linewidth=1,
    label='Граница СПб'
)

# 3. Оформление
ax.set_title("Диаграмма Вороного по станциям метро СПб 2.0", fontsize=14)
ax.axis('off')
ax.legend()

plt.tight_layout()
plt.show()

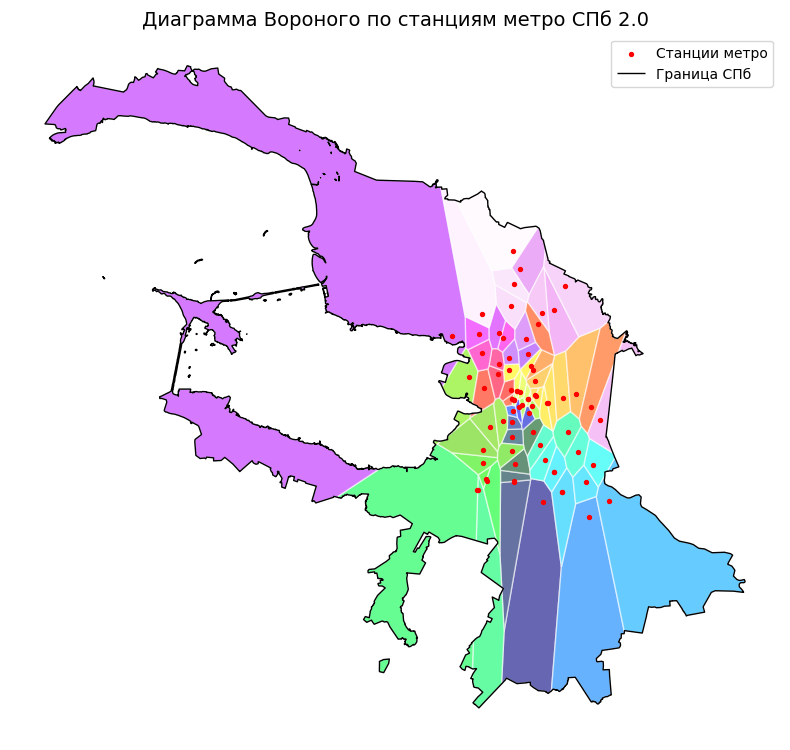
Мы построили классическую диаграмму Вороного по станциям метро — пространство города разбилось на ячейки, каждая из которых показывает зону ближайшей станции. Это наглядно демонстрирует «зоны влияния» метро и помогает быстро оценить доступность станций для разных кварталов. Однако следует помнить, что вычисления основаны на прямом (евклидовом) расстоянии, без учёта реальной уличной сети, барьеров и особенностей рельефа. Поэтому, несмотря на полезную наглядность, для точного анализа доступности стоит использовать инструменты сетевого анализа (с некоторыми из них мы познакомимся в следующие недели)

3. Nearest Neighbour Index

NNI (Nearest Neighbor Index, индекс ближайшего соседа) — это статистическая мера, которая позволяет оценить, насколько равномерно распределены объекты в пространстве. Давайте посмотрим, на распределение театров в Санкт-Петербурге

Прочитаем данные о театрах и подготовим их для последующего анализа

theaters = gpd.read_file('data/spb_theaters.geojson')
theaters = theaters.dropna(subset=['geometry'])  # убираем точки без геометрии

# Перепрецируем в подходящую UTM-зону
utm_crs = theaters.estimate_utm_crs()
theaters_utm = theaters.to_crs(utm_crs)

# Преобразуем геометрические данные в координаты
theaters_coords = np.array([point.coords[0] for point in theaters_utm.geometry])

Производим необходимые вычисления

# 1. Построим матрицу евклидовых расстояний и сразу «забаним» диагональ
dist_matrix = cdist(theaters_coords, theaters_coords, metric='euclidean')
np.fill_diagonal(dist_matrix, np.inf)
nearest_neighbor_distances = dist_matrix.min(axis=1)

# 2. Среднее расстояние до ближайшего соседа
average_nearest_neighbor_distance = nearest_neighbor_distances.mean()

# 3. Площадь Санкт-Петербурга в той же метрической CRS
admin_border_utm = admin_border.to_crs(utm_crs)
admin_area = admin_border_utm.geometry.area.iloc[0]

# 4. Ожидаемое среднее при случайном распределении
n = len(theaters_coords)
expected_mean_distance = 0.5 * np.sqrt(admin_area / n)

# 5. Рассчитываем NNI
NNI = average_nearest_neighbor_distance / expected_mean_distance
print("NNI:", NNI)

NNI: 0.433797191825172

Полученное значение NNI ≈ 0.43 существенно меньше единицы. Это говорит о том, что распределение театров в Петербурге кластери­зовано, а не случайно или равномерно.

4.Итог

1. Мы научились агрегировать пространственные и атрибутивные данные: считали средний, минимальный и максимальный годы постройки МКД по округам Санкт-Петербурга

2. Познакомились с Диаграммой Вороного и построили «зоны влияния» станций метро: каждая точка города отнесена к ближайшей станции по евклидову расстоянию.

3. Узнали об оценке кластеризации точечных объектов с помощью Nearest Neighbour Index.

При этом всегда важно помнить ограничения методов: диаграмма Вороного и NNI опираются на прямое (евклидово) расстояние и не учитывают реальную уличную сеть и препятствия. Для более точных пространственных моделей стоит применять сетевой анализ (с которым мы познакомимся на следующих занятиях).

На основе материалов этого и прошлого занятия вы сможете полностью выполнить второй проект