II. Проекции и системы координат#
Отобразить поверхность Земли на плоскости – самая практическая тема в картографии
В этом разделе мы разберемся, зачем нам нужны картографические проекции и системы координат, почему их так много, и как знания о них помогут избежать ошибок при составлении карт.
А также построим карту плотности населения по округам Санкт-Петербурга и убедимся, что без знаний о системах координат, у нас это бы не получилось сделать
2.1 Краткая теория#
Нам нужно отобразить поверхность земного шара(3D) на плоскости(2D), и, к сожалению, это не получится сделать без искажений.
Чтобы точно убедиться в этом – посмотрите чудесное видео Why all world maps are wrong
Именно поэтому нам нужны … ->
Картографические проекции#
Картографические проекции - способ перехода от реальной, геометрически сложной земной поверхности к двумерной плоскости листа бумаги
При проецировании данных на карте могут искажаться углы, площади и расстояния (что-то одно, или все сразу). В зависимости от типа искажений, проекция может быть равноугольной, равнопромежуточной или равновелкиой, соотвественно (или произвольной)
Ряд проекций рассчитаны для отображения всего Мира, но большинство из них созданы и оптимизированы для небольших частей земли, что позволяет сократить искажения до минимума
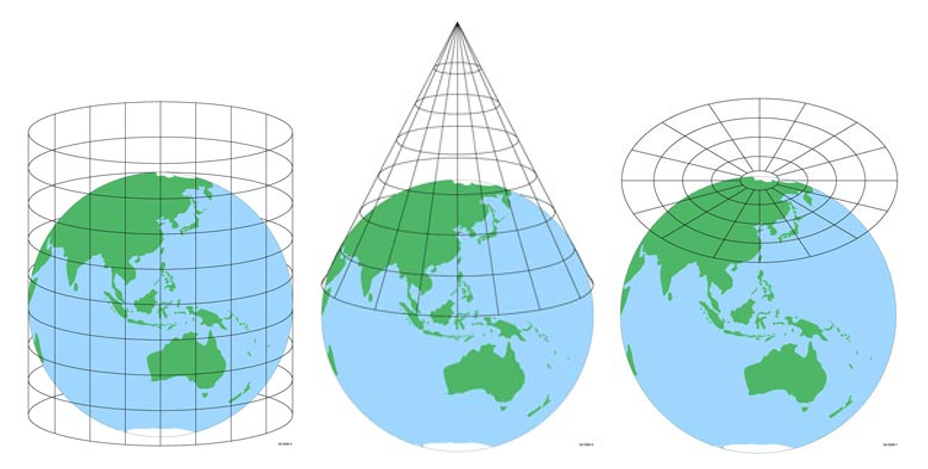
Проекции делать на разные группы на основе того, какая вспомогательная поверхность была использована при переходе от эллипсоида к карте: цилиндр, конус или плоскость
Map Projection Explorer – прекрасная платформа, которая рассказывает о 100 картографических проекциях: какие искажения они имеют, какая вспомогательная поверхность была использована при переходе от эллипсоида к плоскости (цилиндр, конус, лист), как выглядит карта Мира в каждой из них 🗺
Image source: ICSM.gov.au
Универсальная поперечная проекция Меркатора (UTM)#
Универсальная поперечная проекция Меркатора (Universal Transverse Mercator, UTM) - одна из самых распространенных и широко используемых групп картографических проекций.
В ее основе лежит разделение поверхности Земли на 60 полос шириной по 6 градусов долготы каждая (отдельно в северном и южном полушариях, всего - 120). Каждая из этих полос имеет центральную ось, которая служит в качестве опорной линии для проекции.
За счет деления поверхности земного шара на множество отрезков, удается достичь минимальных искажений в пределах каждой зоны UTM.
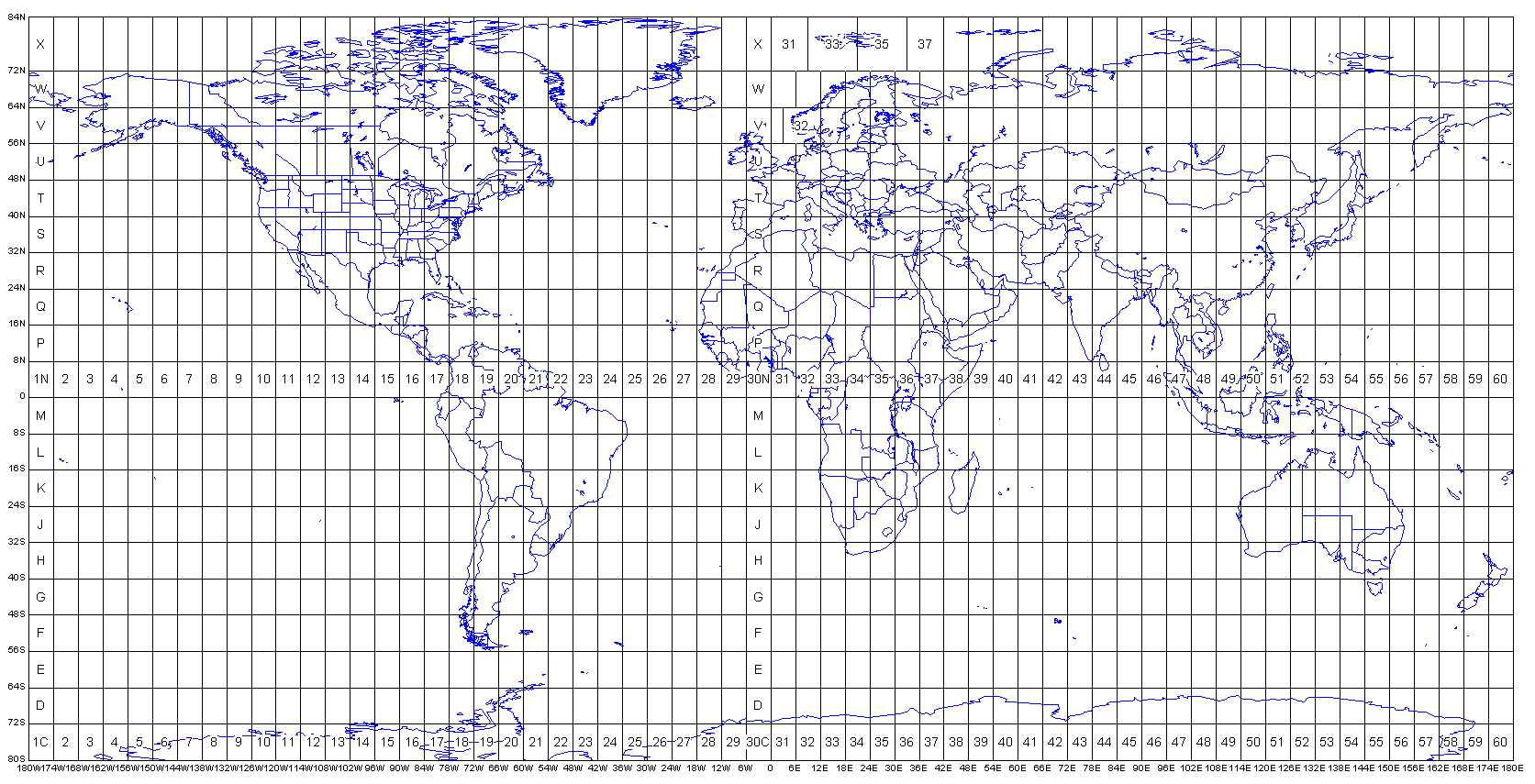Image Source: Dmap.co.uk
Системы координат#
Системы координат(СК) - способ указания местоположения точек на поверхности Земли
Географические системы координат
Географические системы координат знакомы нам еще со школьных уроков географии. Местоположение точки в пространстве определяется значениями широты и долготы в градусах. На основе этих координат вы сможете без дополнительной информации определить местонахождение объекта на карте.
Например, 59°57′ с. ш. 30°19′ в. д. - координаты Санкт-Петербурга <3
Одной из самых распространенных географичеcких систем координат – WGS 84. Большая часть открытых данных, треков с мобильных устройств и пр. будут использовать эту СК.
Прямоугольные системы координат (системы координат проекции)
Системы координат проекции задаются на плоскости двумерной проекции, где каждая точка определяется двумя параметрами относительно центральной - начала координат. Эти параметры называются координатами X и Y.
Лишь по значениям координат точки, но не имея представление о том, в какой проекции данные, вы не сможете определить местонахождение объекта, так как начало координат всегда будет разным.
Единицы измерения - линейные, могут быть выражены метрах/километрах, футах или других единицах измерения.
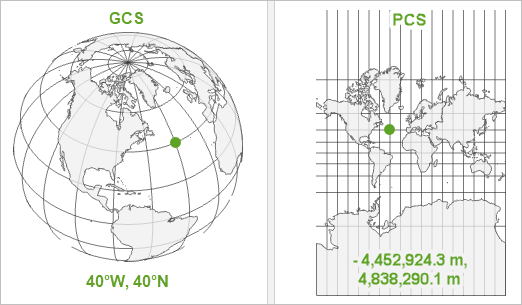Image Source: esri.com
EPSG#
EPSG (European Petroleum Survey Group) коды - это числовые идентификаторы, используемые для однозначной идентификации различных систем координат, проекций и геодезических датумов. Они были разработаны Европейской группой по геодезии и разведке нефти (European Petroleum Survey Group) для использования в нефтегазовой промышленности, но теперь широко используются в геоинформационных системах (ГИС).
Например, самой популярной географической системе координат соответствует код EPSG:4326
Структура кода EPSG для UTM систем координат выглядит следующим образом:
Для северного полушария: EPSG:326xx, где xx - номер зоны UTM
Для южного полушария: EPSG:327xx, где xx - номер зоны UTM
2.2 Практика#
В этом разделе мы попробуем построить карту плотности населения по округам Санкт-Петербурга и убедимся, что даже для такой с виду несложной задачи, важно понимать, как работать с разными системами координат
Импортируем библиотеки
import pandas as pd
import geopandas as gpd
Читаем данные округов Санкт-Петербурга
admin_okrug = gpd.read_file('data/spb_admin.gpkg', layer="okrug")
Узнаем систему координат#
admin_okrug.crs
<Geographic 2D CRS: EPSG:4326>
Name: WGS 84
Axis Info [ellipsoidal]:
- Lat[north]: Geodetic latitude (degree)
- Lon[east]: Geodetic longitude (degree)
Area of Use:
- name: World.
- bounds: (-180.0, -90.0, 180.0, 90.0)
Datum: World Geodetic System 1984 ensemble
- Ellipsoid: WGS 84
- Prime Meridian: Greenwich
Интересно! Давайте разберемся в том, что тут написано:
Это географическая система координат, представленная двумерными координатами (широта и долгота), и ее идентификатор – EPSG:4326
Название СК: WGS 84:
Информация об осях: используются эллипсоидальные координаты: широта (Lat) и долгота (Lon). Единицы измерения – градусы.
Область применения данной системы координат: весь мир
Используемый эллипсоид: WGS 84
Нулевой меридиан: Гринвич
А Вы знали, что Гринвичский меридиан был установлен впервые в качестве нулевого только в 1884 году? Это решение приняли на Международной меридианной конференции в Вашингтоне
Расчет площади полигонов#
Есть метод geometry, который предоставляет нам доступ к геометрии объектов
И у этого метода есть прекрасный метод area, который возвращает площадь объектов
Давайте создадим в admin_okrug новое поле “area”, куда запишем расчеты.
admin_okrug['area'] = admin_okrug.geometry.area
admin_okrug.head()
/var/folders/ry/9bb7wrz54vq_kn2ytlj6ynzm0000gn/T/ipykernel_63225/1718978662.py:1: UserWarning: Geometry is in a geographic CRS. Results from 'area' are likely incorrect. Use 'GeoSeries.to_crs()' to re-project geometries to a projected CRS before this operation.
admin_okrug['area'] = admin_okrug.geometry.area
| NAME | Popul | geometry | area | |
|---|---|---|---|---|
| 0 | округ Пискарёвка | 61706.0 | MULTIPOLYGON (((30.35925 59.99390, 30.37635 59... | 0.001495 |
| 1 | Смолячково | 742.0 | MULTIPOLYGON (((29.42981 60.18954, 29.45195 60... | 0.001283 |
| 2 | Молодёжное | 1685.0 | MULTIPOLYGON (((29.45195 60.20537, 29.45554 60... | 0.002004 |
| 3 | Серово | 272.0 | MULTIPOLYGON (((29.48220 60.22101, 29.48917 60... | 0.001564 |
| 4 | Кронштадт | 44374.0 | MULTIPOLYGON (((29.63402 60.03155, 29.63406 60... | 0.003222 |
И вот тут незадача! Значения странные и очень маленькие. Что же с ними такое?
Давайте вспомним про систему координат этого слоя … она географическая…и единицы измерения в градусах … а значит и все расчеты будут тоже в градусах))
Всегда обращайте внимание на “UserWarning” как при расчете площади выше, там тоже указано, что значения скорее всего будут некорректные, и чтобы получить верные, нужно перепроецировать данные…в данном случае выберем UTM, но перед этим нам нужно понять, в какую зону попадают наши данные
Узнать подходящую UTM зону#
UTM зону можно рассчитать самостоятельно на основе координат точки. Для вычисления номера зоны нам понадобится только долгота, а широта укажет на то, северная это зона или южная.
Напишем небольшую функцию для этой задачи:
def utm_zone(longitude):
zone = int((longitude + 180) / 6) + 1
return zone
Воспользуемся нашей функцией и проверим номер зоны для объекта, который находится на 30.33 градусе восточной долготы
longitude = 30.33
zone = utm_zone(longitude)
print("Номер зоны UTM:", zone)
Номер зоны UTM: 36
На самом деле, выше мы просто потренировались в написании функций, и эту задачу можно решить проще :)
Для набора данных узнать UTM зону можно с помощью метода estimate_utm_crs()
admin_okrug.estimate_utm_crs()
<Derived Projected CRS: EPSG:32636>
Name: WGS 84 / UTM zone 36N
Axis Info [cartesian]:
- E[east]: Easting (metre)
- N[north]: Northing (metre)
Area of Use:
- name: Between 30°E and 36°E, northern hemisphere between equator and 84°N, onshore and offshore. Belarus. Cyprus. Egypt. Ethiopia. Finland. Israel. Jordan. Kenya. Lebanon. Moldova. Norway. Russian Federation. Saudi Arabia. Sudan. Syria. Turkey. Uganda. Ukraine.
- bounds: (30.0, 0.0, 36.0, 84.0)
Coordinate Operation:
- name: UTM zone 36N
- method: Transverse Mercator
Datum: World Geodetic System 1984 ensemble
- Ellipsoid: WGS 84
- Prime Meridian: Greenwich
Отлично! Теперь мы знаем, что для нашего набора данных с округами Санкт-Петербурга подойдет зона 36N!
Перепроецирование#
Благодаря estimate_utm_crs() мы знаем нужную нам систему координат. Давайте запишем ее в отдельную переменную, чтобы в дальнейшем можно было использовать при перепроецировании данных
data_crs = admin_okrug.estimate_utm_crs()
Для перепроецирования мы воспользуемся методом to_crs(), внутри которого укажем целевую СК
admin_okrug_utm_36N = admin_okrug.to_crs(data_crs)
print(admin_okrug_utm_36N.crs)
EPSG:32636
Отлично! EPSG:32636 - 36N зона UTM
Расчет площади 2.0#
Попробуем еще раз рассчитать площадь округов Санкт-Петербурга и посмотрим на получившиеся значения
admin_okrug_utm_36N['area_new'] = admin_okrug_utm_36N.geometry.area
admin_okrug_utm_36N.head()
| NAME | Popul | geometry | area | area_new | |
|---|---|---|---|---|---|
| 0 | округ Пискарёвка | 61706.0 | MULTIPOLYGON (((352703.954 6653672.464, 353647... | 0.001495 | 9.292112e+06 |
| 1 | Смолячково | 742.0 | MULTIPOLYGON (((302068.083 6677873.169, 303389... | 0.001283 | 7.933135e+06 |
| 2 | Молодёжное | 1685.0 | MULTIPOLYGON (((303389.678 6679568.341, 303601... | 0.002004 | 1.238612e+07 |
| 3 | Серово | 272.0 | MULTIPOLYGON (((305157.564 6681218.991, 305563... | 0.001564 | 9.662041e+06 |
| 4 | Кронштадт | 44374.0 | MULTIPOLYGON (((312486.108 6659698.584, 312488... | 0.003222 | 2.002856e+07 |
Теперь похоже на правду и это квадратные метры!
Такая запись может быть не всем знакома, давайте разберем ее на одном из примеров: 9.292112e+06 - это то же самое "9.292112 умножить на 10 в степени 6", то есть 9292112 квадратных метра или 9.3 квадратных километра
Карта плотности населения#
Посчитаем плотность в “человеках на квадратный километр”, запишем это в новое поле “pop_density” и посмотрим на результат
admin_okrug_utm_36N.eval('pop_density = Popul / (area_new / 1000000)', inplace=True)
admin_okrug_utm_36N.head()
| NAME | Popul | geometry | area | area_new | pop_density | |
|---|---|---|---|---|---|---|
| 0 | округ Пискарёвка | 61706.0 | MULTIPOLYGON (((352703.954 6653672.464, 353647... | 0.001495 | 9.292112e+06 | 6640.686076 |
| 1 | Смолячково | 742.0 | MULTIPOLYGON (((302068.083 6677873.169, 303389... | 0.001283 | 7.933135e+06 | 93.531751 |
| 2 | Молодёжное | 1685.0 | MULTIPOLYGON (((303389.678 6679568.341, 303601... | 0.002004 | 1.238612e+07 | 136.039328 |
| 3 | Серово | 272.0 | MULTIPOLYGON (((305157.564 6681218.991, 305563... | 0.001564 | 9.662041e+06 | 28.151402 |
| 4 | Кронштадт | 44374.0 | MULTIPOLYGON (((312486.108 6659698.584, 312488... | 0.003222 | 2.002856e+07 | 2215.536304 |
Построим статичную карту с помощью метода plot, на которой значения плотности населения отобразим с помощью картограммы
Картограмма - это способ картографического изображения, иллюстрирующий относительные показатели в пределах административного деления. Интенсивность значений показателя передается с фоновой окраски или штриховки. В английском языке картограмма - choropleth. Про другие способы изображения можно почитать в этой статье
admin_okrug_utm_36N.plot(column='pop_density', cmap='viridis', legend=True)
<Axes: >
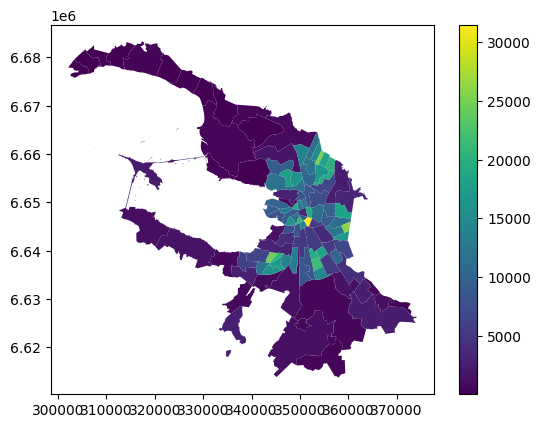
Создадим интерактивную карту, как в предыдущем разделе
admin_okrug_utm_36N.explore(column='pop_density', cmap='viridis', legend=True, tiles='cartodbpositron')
Готово!
2.3 Установка системы координат#
Для данных без СК#
Иногда бывают случаи, когда нам нужно определить систему координат у пространственных данных. Посмотрим на примере csv с театрами в Санкт-Петербурге.
Прочитаем данные и создаим на их основе GeoDataFrame:
theaters = pd.read_csv('data/spb_theaters.csv')
theaters[['latitude', 'longitude']] = theaters['coord'].str.split(',', expand=True)
theaters_gdf = gpd.GeoDataFrame(theaters, geometry=gpd.points_from_xy(theaters['longitude'], theaters['latitude']))
Провертим систему координат theaters_gdf
print(theaters_gdf.crs)
None
None - потому что мы не установили ее при создании GeoDataFrame! Но бывает, что к нам просто попадают данные без СК.
В этих случаях мы можем задать ее с помощью метода set_crs (вариант 1) или приравняв crs данных к нужной системе координат (вариант 2)
theaters_gdf = theaters_gdf.set_crs(epsg=4326) # вариант 1
theaters_gdf.crs = "EPSG:4326" # вариант 2
print(theaters_gdf.crs)
EPSG:4326
Установка системы координат VS перепроецирование#
Во время перепроецирования происходит пересчет координат из одной системы координат в другую – меняется СК у набора данных и перезаписываются координаты для всех объектов.
Если мы устанавливаем систему координат, то в этот момент пересчет координат не происходит, у нас просто перезаписывается определение системы координат у данных
При установке СК важно понимать, в какой СК представлены координаты объектов, и если выбрать неправильную, то данные могут оказаться в разных точках земного шара
2.4 Выбрать проекцию для карт#
Наиболее распространенной проекцией для ГИС проектов, связанных с городскими данными, является универсальная поперечная проекция Меркатора (UTM).
Для более мелких масштабов, например, чтобы отобразить границы России или весь Мир, задача подбора необходимых проекций стоит значительно сложнее и во многом зависит от территории и задач Вашей работы.
Есть прекрасная книга 1987 года Map Projections – A Working Manual📕, в которой можно найти подробное описание разных типов проекций, их особенности, историю и применение
Итоги#
Мы коротко рассмотрели теорию о проекциях и системах координат. Это ключевая тема при работе с пространственными данными. На простом примере создания карты плотности населения в Санкт-Петербурге убедились, что знания об особенностях систем координат очень важны для получения корректного итогового результата.